Two rhombuses PQRS and MLKJ have sides calculated as follows: Side of rhombus PQRS is calculated using the formula 6 2 + 8 2 = 10 = 5 cm \sqrt{\frac{6...

Banking SBI PO Mains Medium Verbal Reasoning MCQ

Question

Two rhombuses PQRS and MLKJ have sides calculated as follows:

Side of rhombus PQRS is calculated using the formula $\sqrt{\frac{6}{2} + \frac{8}{2}} = \sqrt{10} = 5 \text{ cm}$ .
For rhombus MLKJ, given $\sin 30^\circ = \frac{\text{perpendicular}}{\text{hypotenuse}} = \frac{1}{2} = \frac{7.5}{\text{side of MLKJ}}$ , the side of MLKJ is found to be $15 \text{ cm}$ .

If AB is the side of PQRS and CD is the side of MLKJ, what is the length of the median XY of trapezium ABCD formed by these sides?

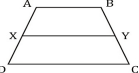
Screenshot 2025-09-03 01.54.55.png

Calculate the median XY using the formula:

XY = \frac{AB + CD}{2}

$7.5 \text{ cm}$

$10 \text{ cm}$

$12.5 \text{ cm}$

$20 \text{ cm}$

geometryrhombusmediantrapeziumtrigonometry

Get instant feedback with detailed step-by-step solution